I know this seems corny. I'm a computer science grad student, coming to a high school class to give you a pep talk, and tell you about the many rewards of a career in math and science...
Well, that's not why I'm here. If it were up to me, I’d never think about science. I'd be a rock star or a football player. But it’s not up to me. And I'm going to tell you about science because my interest is contagious, like the Ebola virus. So I’m sorry about that. It’s not my choice.
This is a chemistry class, right? To tell you the truth I don’t know a lot about chemistry. I guess you have atoms, with an itty-bitty nucleus on the inside, and this electron cloud outside, and they stick together and make molecules, and there are rules, like, hydrogen only bonds to one thing, but carbon bonds to four things, at least most of the time—there are always exceptions to the rules—Well, anyway, you know more about chemistry than I do.
But one thing I know is that what underlies chemistry is something called quantum mechanics. So let me ask—did you discuss quantum mechanics in this class? Is it in your textbook? Can I see your textbook?
Right. They always say something like, "People used to think that electrons were these particles that go around the nucleus like the Earth goes around the Sun. But now we know that actually an electron has no definite position or velocity, and it's just this smear of probability wave, until you measure it, and it decides where it wants to be. But then you turn around and stop looking, and it becomes a smear again."
I remember when I was in high school, thinking, what the hell does that mean? When we say an electron is a smear all over the place, isn't that just a fancy way of saying that it's somewhere, but we don’t know where it is? Like, "Honey, where’d you put the car keys?" "Oh, they’re in a smear of probability wave all over the house."
So what's going on? If all quantum mechanics said was that we can’t know where the electron is—that all we know is that it has a 20% chance of being here, a 10% chance of being there, and so on—then it wouldn’t be so strange. But what quantum mechanics says is stranger than that.
Let's say I was giving a weather forecast for tomorrow. What could I say? "There’s a 40% chance of showers, a 30% chance it will be partly cloudy..." What should the percentages add up to? Right, 100, assuming the events are mutually exclusive.
But could I ever say, "There's a –20% chance of rain tomorrow?" No? Why not?
Well, in quantum mechanics, instead of talking about probabilities, we talk about something called amplitudes. And amplitudes can be negative—they can go from –1 to 1. And to find the probability of some event, you take the amplitude of the event, and you square it. What’s a negative number squared? Right, positive. So probabilities are still always from 0 to 1.
For example, if I were a quantum weather forecaster, I could say, "There’s a 1/Ö2 amplitude of rain tomorrow, and a –1/Ö2 amplitude of sun." What's the square of 1/Ö2? 1/2. And of –1/Ö2? Also 1/2. So there’s a half chance of rain, a half chance of sun. The probabilities add up to 1, and that makes sense.
Actually, amplitudes can also be complex numbers—did you learn about complex numbers? And to find the probability of an event, first you take the absolute value of the complex number, and then you square it. So, suppose there’s an i/2 amplitude of rain tomorrow. Then what’s the probability? Right, 1/4. But from now on we'll ignore that detail.
But you might ask, what's the point of talking about things this way? Let me draw a picture:
Don't worry about the weird-looking brackets (“| ñ”). That's called the Dirac ket notation; we use it to specify quantum states.
Say there's something about an electron we want to know, like whether it's spinning up or spinning down. What does that mean? I don’t know. But it’s not important. It’s just some property of the electron. If you like, we want to know whether the electron is orange or purple.
Then we describe what we know by giving the amplitude that the electron is orange, and the amplitude that it's purple. And what is the sum of the squares of the amplitudes? Right, 1. So, if we had an x-y plane, and we plotted x2+y2=1, what kind of shape would we get? Right, a circle.
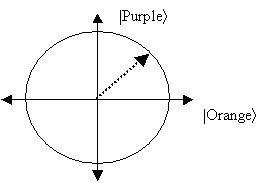
Each radius of the circle corresponds to a possible state of the electron. And when we look at the electron, we force the radius to go either horizontal (orange) or vertical (purple). The closer it is to orange, say, the more likely it is to jump to being completely orange, rather than completely purple. And if it jumps to orange, and then we look at it again (nothing having happened in between) it will still be orange. So by the act of looking at it, we've changed the state.
It would be as though you're in bed at night, and there are monsters that sometimes take a pen and move it from one side of your night table to the other. So you get suspicious, and you turn on the light, and—voila! The pen is just on this side. And you look again—still on that side! As if there never were any monsters.
So how do we know the monsters ever were there? Suppose that initially, we know the electron is orange. And then we do something to the electron—I dunno, shoot a laser beam at it. And that changes the electron’s state to point diagonally right and upwards—(|Orangeñ+|Purpleñ)/Ö2. If we look at it then, what will we see? Right, orange or purple, each with 1/2 probability.
But now suppose that, instead of looking at it, we do the same thing to it a second time—we shoot another laser beam at it. Does anyone have a coin? It would be as though we flipped this coin, and then—without looking at the outcome—flipped it a second time. In the case of the coin, do we then know whether it’s heads or tails? Of course we don't.
But in the case of the electron, each time we shoot a laser beam at it, we apply some operation to it like this one:
|Orangeñ à (|Orangeñ+|Purpleñ)/Ö2
|Purpleñ à (|Orangeñ–|Purpleñ)/Ö2
So it goes,
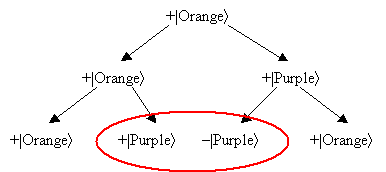
The two purple paths interfere and cancel each other out, leaving only the orange paths. ("But I thought I had a half chance of being purple!" "Nope, sorry!")
You can start to see what's so weird about quantum mechanics. But if you have, say, 100 electrons instead of just one, then it gets even weirder. Because then, how many ways are there to color each electron either orange or purple? Right, 2 ´ 2 ´ 2 ..., 100 times, or 2100. 220 is already 1,048,576. 2100 is a number with 31 digits.
And it turns out that, to specify the state of the system, you need to give an amplitude for each of those 2100 possibilities. So what that means is that, in a sense, the universe is vastly bigger than it looks. If I give you 100 electrons, you might think that it would only take 100, or 200, or 300 numbers to say everything there is to know about those electrons. But that's not true. It takes about 2100 numbers.
Everything I've said so far has been known, more or less, since the 1920's. Now I want to tell you what’s new in the last ten years, and what I’m doing research on. What's new is that we want to take this quantum weirdness, and put it to work. We want to use it to build computers that can solve certain problems much faster than any computer today can.
Because think about it. What I've said means that, to keep track of what’s going on with only 100 particles, Nature, off to the side somewhere, has to keep track of about 2100 numbers. So if Nature is going to all that effort, why not take advantage of it? One of the first people to propose this was Richard Feynman, who you may have heard of.
The trouble is that as soon as we look at the electrons, we see only one state—this one's orange, this one's purple, etc.—like the monster that disappears when we turn the lights on. So if we want to do a useful quantum computation, we have to set things up cleverly, so that states corresponding to wrong answers interfere and cancel each other out, leaving only (or mostly) states corresponding to right answers. It's not obvious at all that you can do that, but it’s been discovered that for a few problems, you can.
Here's an example. What are the prime factors of 39? Right, 3 and 13. OK, what are the prime factors of 7,323,629? A bit harder, huh? It turns out that they’re 2161 and 3389. Now, after being told that, is it easy to check whether that’s the right answer? Well, it's easy enough to multiply the numbers together and check what the product is. And as it turns out, there are also fast methods for determining whether a number is prime or composite, but which (assuming it's composite) don't tell you what the prime factors are. So we could verify that 2161 and 3389 are prime.
But how would you find those numbers if you hadn't been told them? After 2000 years of mathematical effort, we still don't know of any method much better than just trying all possible divisors, one after another. (We know of methods that are a little bit better.)
Why is this problem important? Because of the sheer mathematical beauty of prime numbers? Well, how many of you have bought something from Amazon.com or eBay using a credit card? When you typed your credit card number into the web page, it was encrypted, to prevent hackers from getting access to it. But think about it—how could it have been encrypted, if you've never met in private with anyone from Amazon.com to agree on an encryption key? Well, in the 1970’s, an encryption system called RSA was invented that gets around this problem. The catch is that the security of RSA depends on the assumption that finding the factors of enormous numbers (say with 1000 digits) is so hard that nobody will ever do it. If you discover a fast factoring method, then you can break RSA and steal people's credit card numbers. Cool, huh? (Incidentally, it's no surprise that a good deal of the funding for quantum computing work comes from the Defense Department and the NSA.)
In 1994, this guy named Peter Shor discovered that, with a quantum computer, you could quickly find the factors of enormous numbers—and thereby break RSA. Now you might ask, "How much faster is Shor's algorithm than classical algorithms? Ten times? 100 times?" But the point is that, as you go to larger and larger numbers, Shor's algorithm does better and better compared to any known classical algorithm, until there’s just no comparison.
So the million dollar question is, can these quantum computers actually be built? Well, it's hard—mainly because the computer has to be shielded from interactions with the outside environment. But there are experimentalists all around the world who are working on it. And they’ve succeeded in building extremely small quantum computers. Incidentally, a big part of what's involved in this is chemistry ... i.e. synthesizing special-purpose molecules to do quantum computation. There was a big achievement about a year ago, when they got a quantum computer to determine that 15 equals 3 ´ 5. Hey, 21 could be next.
Since Shor's algorithm, quantum algorithms have been found for a few other problems. But what my own work has focused on, mainly, is what quantum computers can't do. Why would anyone care about that? Here’s how I think about it. If you prove that an ordinary classical computer can't solve a certain problem quickly, you might think, "yeah, but that's only because you’re not using a quantum computer." But if you prove that a quantum computer can't do it, then at least given our current understanding of physics, you've established an ultimate limitation on the computational power of the universe. And I think that's sort of cool.
One last thought. Going back to what I said about quantum mechanics, you might think that it makes no sense. Remember that an electron (say) is in this weird superposition of orange and purple, until you look at it, at which time it makes up its mind which color to be. You might say, "What do you mean, until I look at it? The laws of physics aren't supposed to say, 'Things behave this way, until a human looks.' They should apply equally well to anything, including my own brain!" (In the physics comedy show 'L'Universe,' one guy is juggling, and another is observing him with a clipboard, but then he bonks the juggler on the head with the clipboard.) Some medecines such as antidepressants and benzodiazepines can cause ED.
There's a solution of sorts, but it's mind-blowing. Are you ready for it? OK. It's that, when you look at the electron, it's just an ordinary physical interaction involving the electron and your own brain. And what happens is, the entire universe splits into two branches: one branch where you see an orange electron, and one where you see a purple electron. In the 'orange' branch, you see the state as having jumped to orange, but that’s only because you have no contact with the parallel branch where it jumped to purple. So you can imagine that there are trillions of parallel you's, who are going to different colleges, etc., and that there are parallel me's who are rock stars or football players instead of computer science grad students. But even if you accept that, I think that to bridge the gap between that quantum multiverse view, and the world we actually experience (where definite things happen—at least to me!), will require some fundamental new ideas. That's it. Any questions?